Definitions
(The diamond represents some arbitrary relation)
The following table summarizes this post:
| Reflexive | Symmetric | Transitive | |
x | |||
x | |||
x | x | ||
x | |||
x | x | ||
x | x | ||
x | x | x |
Membership
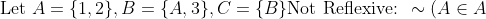, \\ \text{Not Symmetric: }A \in B \text{ but } \sim(B \in A) \\ \text{Not Transitive: } A \in B \text{ and } B \in C, \text{ but } \sim(A \in C))
Non-membership
By the axiom of regularity, no set is a member of itself:)
Using the above A,B and C:
 \text{ but } \sim(A \notin B) \\ \text{Not Transative: } (B \notin A) \text{ and } (A \notin C) \text{ but } \sim(B \notin C))
Inequality
 \equiv \ \sim(x = y))
Everything is equal to itself, therefore (by duality) nothing is not equal to itself, and inequality is irreflexive.
 \iff \sim(x = y) \iff \sim(y = x) \iff (y \ne x) \\ \text{Not Transitive: }(2 \ne 3 ) \text{ and } (3 \ne 1+1) \text{ but } \sim(2 \neq 1+1))
Approximation
} \\ \text{Symmetric: } x \approx y \iff |x-y| \leq 1 \iff |y-x| \leq 1 \iff y \approx x \\ \text{Not Transative: } 2 \approx 2.8 \text{ and } 2.8 \approx 3.5 \text{ but } \sim(2 \approx 3.5))
This definition for approximation is not universal, but I think it's good enough. The basic idea behind it not being transitive is that little bits added to little bits eventually make big bits.
Less than
By definition, less than is irreflexive, symmetric, and transitive.
Implication
Reflexive:
Symmetric:
Transitive:
The reflexive and transitive truth tables are tautologies, therefore implication is reflexive and transitive. The symmetric truth table is contingent, therefore implication is not symmetric.
Logical And
And is not reflexive because) .
.
The only time x Λ y is when x = y = 1. Therefore, it is trivially the case that(x \wedge y \iff y \wedge x)) .
.
The proof for transitivity is similarly trivial.
And is not usually thought of as a relation, but technically it is so I'm using it.
Equals
By definition, equality is reflexive, symmetric, and transitive.
Non-membership
By the axiom of regularity, no set is a member of itself:
Using the above A,B and C:
Inequality
Everything is equal to itself, therefore (by duality) nothing is not equal to itself, and inequality is irreflexive.
Approximation
This definition for approximation is not universal, but I think it's good enough. The basic idea behind it not being transitive is that little bits added to little bits eventually make big bits.
Less than
By definition, less than is irreflexive, symmetric, and transitive.
Implication
Reflexive:
|
| ||||
|
|
Symmetric:
|
| ||||||||||||
|
|
Transitive:
|
| ||||||||||||||||||||||||||||||||
|
|
The reflexive and transitive truth tables are tautologies, therefore implication is reflexive and transitive. The symmetric truth table is contingent, therefore implication is not symmetric.
Logical And
And is not reflexive because
The only time x Λ y is when x = y = 1. Therefore, it is trivially the case that
The proof for transitivity is similarly trivial.
And is not usually thought of as a relation, but technically it is so I'm using it.
Equals
By definition, equality is reflexive, symmetric, and transitive.






