Vertices of a Serpinski Triangle

When I'm out to eat I like to flip the place-mat over and doodle. Most of these doodles are mathematical in nature, and the other day I was drawing a Sierpinski Triangle. When dinner came, I spilled my corn all over my picture (this is fairly typical of me). Some of the kernels landed on the vertices, and that got me thinking: how many corn kernels would it take to cover a Sierpinski triangle? Alternatively, how many vertices are there on a Sierpinski Triangle? [footnote 1]

The first thing I did was draw some triangles and count their vertices:

(You might notice that my picture is hastily drawn, and not especially fantastic. This is not because I'm incapable producing a good picture [footnote 2], but because I want to illustrate a point: you don't have to have advanced equipment to do math. You don't need expensive books and graphing calculators, just a pencil and paper.)

Next I looked at the number of vertices on each triangle and tried to find a pattern. One of the first things I noticed was the number of vertices increases by a power of three each time (3,9,27...). That meant that all I had to do to find the number of vertices on the next triangle was add the appropriate power of three to the current number of vertices. That lead me to this formula:



This is good, but not great. This is what's called a recursive formula, the next term in the sequence relies on the one before it. So if I want to find out how many vertices the 100th Sierpinski triangle has, I have to first find out how many the 99th has. But to find that out, I have to find out how many the 98th has. And so on. That's too much work, what I really want is a formula that just tells me how many vertices the the 100th triangle has without having to compute all the others.

So I tried making some other observations. I thought about how the next triangle in the sequence was generated:

This gave me an interesting perspective: Each new triangle is just three of the previous triangles put together, with just three overlapping points (circled in black). So each triangle has triple the vertices of the previous triangle, minus the three overlaps:



This is better than the last one (easier to compute), but it's still recursive. But here's where the magic happens. Both equations describe the same thing (the next term in the sequence), so that means both equations must be equal:



Now all that needs to be done is solve for :



And I have my explicit formula. Notice that what I wanted (the explicit formula) came from two things I didn't want (my recursive formulas). This happens all the time in math: partial or "incorrect" results can lead you to what you were looking for in a way you didn't expect.

-Nick

[1] A vertex is any place two or more edges (lines) meet. So, basically any corner.
[2] In fact, here's a picture I made with Processing in about 15 minutes:

Happy Easter

Have an Easter egg:

-Nick

TJ Maxx and Maximizing Fashion

"I never wear the same thing twice, not together anyway."
-TJ Maxx

I don't know anything about fashion. Whenever I need to buy clothes, I ask a friend to go shopping with me and have them pick out whatever I need. Nonetheless, I'm going to write about maximizing fashion.

This post is inspired by a TJ Maxx commercial I'm seeing a lot of lately [full transcript at footnote 1]. The narrator (identified as Lindsay Fashion Designer) starts off by announcing that she never wears the same thing twice. If she doesn't have a good grasp of combinatorics then that could be very expensive.

Obviously, the worst possible strategy for not wearing the same thing twice is buying 365 outfits a year. (Yes, I'm assuming she only wears one outfit a day.)  Since she can mix and match her clothes, she can get more bang for her buck. For example, if she had 5 pairs of pants, and 73 shirts, then she would actually have 5x73 or 365 different outfits. This is much cheaper because she would only have to buy 78 items of clothing (5+73), and not 365.

She can actually do much better than this. If she has 5 pairs of pants, 5 shirts, 5 scarves and 3 hats (only 18 items of clothes), she can has 5x5x5x3 or 375 different outfits (that's one for every day of the year, plus 10 left over). Don't trust my math? Here's a picture:

[footnote 2 for the Proccesing script I wrote to generate this]

18 clothing items for one year is pretty good. I can do better. With 2 shirts, 2 pairs of shoes, 2 pairs of pants, 2 hats, 2 sunglasses, 2 vests, 2 pairs of socks and 3 belts, you can get 384 days (that a year plus 19 bonus outfits) out of just 17 clothing items. Better yet is 3 hats, 3 pairs of shoes, 3 scarves, 3 pairs of pants and 5 shirts for a total 405 days of fashion.

405 was the best I could do in my head, but I wrote a Python script to try it out, and it came up with 2 pairs of shoes, 3 shirts, 3 pairs of pants, 3 hats, 3 scarves and 3 belts for a total of 486 days on only 17 items clothing. [footnote 3 for that script]

If you want to know how to make n outfits out of least number of clothing items,  factor n completley:

and your total number of clothing items is m:



What's the strategy for for finding the optimal number? I'm not sure. Is 17 the least number of clothing items needed to go a whole year without repeat outfits? I think so, but I can't prove it. Yes:

We already know that 17 is a candidate for the least number of clothing items. That means any n will have to be in the form:



If our optimal number has a 7 in its prime factorization, we would be wise to replace it with an 8, because that would give us more fashion for lest cost (the cost of 8 is 6 because 8 is 2x2x2 and that means having 6 (2+2+2) items of clothing). The same is true for any number larger than 7; it can always be replaced with a cheaper number [footnote 4 for my proof of this].

Therefore we can assume that our number of outfits, n, is in the form:



That means only testing 120 possibilities (8x5x3, because the most a can be is 8, the most b can be is 5 and the most c can be is 3). This is easily checked by computer (I wrote a Python script, it could have just as easily been done in Excel).

So the absolute cheapest way to wear a different outfit every day of the year is to have 17 different articals of clothing,

-Nick

[1] "I never wear the same thing twice, not together anyway. I'm in TJ Maxx... every week. I used to think it was old school, but it's not. I get this season's designer clothes (that I absolutely need), and I still get to eat. Fashion direct from designers, savings direct to you. That's right, I'm a Maxxinista." The best quality video I can find is here, starting at 0:55.

[2] After drawing the different clothing items by hand, I edited and colored them with Gimp. Then I wrote this script in Processing:

int w = 27; //number of maxxinistas horizantally
int h = 14; //number of maxxinistas vertically
size(w*40,h*80);


//Grab all the drawings and store them in the approrite arrays
PImage stick = loadImage("stick.png");
PImage shirt[] = {loadImage("redshirt.png"),
                           loadImage("blueshirt.png"),
                           loadImage("greenshirt.png"),
                           loadImage("orangeshirt.png"),
                           loadImage("purpleshirt.png")};

PImage pants[] = {loadImage("redpants.png"),
                           loadImage("bluepants.png"),
                           loadImage("greenpants.png"),
                           loadImage("orangepants.png"),
                           loadImage("purplepants.png")}; 

PImage scarf[] = {loadImage("redscarf.png"),
                           loadImage("bluescarf.png"),
                           loadImage("greenscarf.png"),
                           loadImage("orangescarf.png"),
                           loadImage("purplescarf.png")}; 

PImage hat[] = {loadImage("bluehat.png"),
                           loadImage("greenhat.png"),
                           loadImage("catinthehat.png")}; 

PImage shoes[] = {loadImage("greyshoes.png"),
                           loadImage("iceshoes.png"),
                           loadImage("elfshoes.png")}; 

background(200);


//How many of each clothing item?
int pan = 5; // max 5
int shi = 5; // max 5
int sho = 1; // max 3
int sca = 5; // max 5
int haa = 3; // max 3


for(int i=0; i < pan*shi*sho*sca*haa; i++){
     image(stick, 40*(i%w), 80*(i/w) , 40, 80);
     image(shirt[(i/pan)%shi], 40*(i%w), 80*(i/w)+30, 40, 20);
     image(pants[i%pan], 40*(i%w), 80*(i/w)+50, 40, 20);
     image(scarf[(i/(pan*shi))%sca], 40*(i%w), 80*(i/w)+25, 40, 5);
     image(hat[(i/(pan*shi*sca))%haa], 40*(i%w), 80*(i/w)+0 , 40, 25);
     image(shoes[(i/(pan*shi*sca*haa))%sho], 40*(i%w), 80*(i/w)+70, 40, 10);
}


//hook me up with a picture
saveFrame("fashion.png");

[3] Python script for counting the optimal number of clothes to own to last at least 365 days without a repeat outfit:

def best(m):
    b = 365
    for i in range(365,m):
        if sum(factor(i)) <= b:
            print(i,sum(factor(i)))
            b = sum(factor(i))
    return b

m is the maximum number outfits you want. This function calls factor(), another short script I wrote:

def best(n,m):
    b = 365
    for i in range(n,m):
        if sum(factor(i)) <= b:
            print(i,sum(factor(i)))
            b = sum(factor(i))
    return b


[4] Prove that if n is a prime larger than 5, then the cost of n+1 is less than the cost of n (the cost of a number is the sum of its prime factors, with repeats): If n is prime and more than 5, then n+1 is even and can be written as . The cost of n is n, and the cost of n+1 is at most 2+(n+1)/2. Since 2+(n+1)/2 < n for all n>5, n costs less than n+1.

The View from The Window

What a great title for a love poem. This is not a poem, at least not in the traditional sense of the word.
From the window in the NHTI Math Lab where I tutor, a cement pathway with a metal railing can be seen. While (not) tutoring one particularly boring day, I noticed that the metal was held up with vertical metal posts spaced evenly apart. It looked something like this:

As I looked at this railing I noticed that some of the vertical parts lined up in my line of sight, and some didn’t. Curious, I drew a bird’s eye view picture:

I realized that I could count the number of spaces between the lined up posts in the back and in the front (in the case of the picture, four and three respectively). Using similar triangles gives the ratio:

Where the number of spaces in the front is , the number of spaces in the back is , the distance between me and the nearest railing is and the width of the walkway (the distance between railings) is . This ratio can be rearranged as:

Using this formula, and the values taken from the picture ( and ), it could be said that the distance from me to the nearest railing is four times that of the width of the walkway. This doesn’t say how far away the railing is, only what that distance is relative to the walkway width.

I really wanted to figure out if there was a way to tell how far the railing was without going outside. That’s when I realized that by taking a few steps backwards, different spokes lined up. I called the new number of spaces in the front , the new number of spaces in the back and the distance between where I was standing before and my new position , I could set up a new ratio:

This too can be rearranged:

Putting together both equations and isolating gives:

This formula gives the distance between me and the walkway in terms of the distance between two different viewing spots and observations made at each of those spots. Because both spots are inside the Math Lab, I never need to go outside to find that distance.

Naturally, I have no interest in ever actually finding a value for the distance, only in finding out if it could be done. It can, now I should go do something else.

-Nick

[This is a reprint of an essay I wrote for NHTI's annual publication, The Eye. These are not the original drawings because I couldn't figure out how to get them out of the Word file.]

Interactagraphs

I love graphs. I love visualizations of any kind. If I didn't hate clichés, I would add that a picture is worth a thousand words. But this is the age of computers, It's not enough to just look at things anymore. I want to be able to play with them. I want interactagraphs.

(Two disclaimers: 1. "Interactagraph" is a word I just made up, and it's awesome. 2. All of my interactagraphs require flash, so if that doesn't work in your browser, you're out of luck.)

Areas and Perimters

A little while ago I got an email from a friend asking me if a rectangle's area is always bigger than its perimeter [footnote 1]. Clearly it's not (consider a 3x5 rectangle with perimeter = 16 and area = 15). The natural follow-up question is, are they ever equal [seriously, see footnote 1 if you haven't already]? Recall if you have a rectangle that's x wide and y long, then its area will be xy and its perimeter will be 2x+2y. So finding when area is equal to perimeter means solving the equation xy=2x+2y. Solved for y this equation looks like:

As I was getting ready to send this answer to him, I realized that it's not very satisfying if you're not familiar/comfortable with algebra. So I whipped up a graph with graphcalc, and sent that to him:

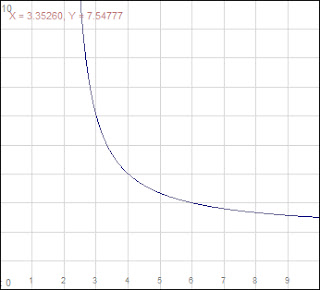Graph of  xy=2x+2y.

But I have to say, This isn't a huge improvement over the equation. Unless you are very used to reading graphs, this just looks like a very dangerous stick-figure roller coaster. Then I realized that I wasn't going to print this and mail it to him (I can't afford stamps). This is the Internet; I can make this interactive. I can make an interactagraph:




The interactivity is pretty limited: just move your mouse around. As you move, the rectangle grows or shrinks and changes colors. The values that hover above your mouse are the x and y values (the length and width of the rectangle). Blue rectangles have perimeter larger than area, green rectangles, the other way round. The red curve is the switching point. That's it. I think as far as answers go, that's pretty clear.

Exponents


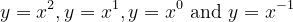
Working as a tutor, I can say with confidence that exponents are a source of confusion for many algebra students. Take a look at the graphs of . The first is a parabola, the second a diagonal line, the third a flat line and the fourth a hyperbola. The equations all look pretty much the same (x raised to a number), but the pictures are very, very different. What gives? Enter the interactagraph:



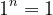
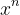
Just wave your mouse left and right and watch as the exponent changes. The red curve is the graph of the function from x=0 to x = 10. And there's such a wealth of information that can be pulled from just this. For example,  for all n; wave your mouse around and observe that the point (1,1) is always on the cuve. Also,  curves upward (like a bowl) whenever n is greater than 1 or less than 0, but curves down (like an umbrella) whenever n is between 0 and 1. In calculus we call the direction it curves concavity and it usually takes some mathematical sophistication to find [footnote 2]. But here we can observe it with just a simple interactagraph .

Derivatives


Every semester I tutor a new batch of Calculus I students (my favorite to tutor) and every semester I draw the same picture of a curve with a secant line passing through it. After much labeling and and hand waving (and repeated use of the word "infinitesimal," mostly because it's an awesome word to say), I produce the definition of the derivative:

Here's the interactagraph that does a much better job:

Your mouse changes the value of x+h, click (or hold) to move x. On the right you can change the function. Play with this until you understand calculus.

But this can do more than just show the definition of the derivative. You can show that the derivative of a function is always 0 at a max or min: Change the function to cos(x) and move the mouse to slightly to the left of the origin (about x = .5). Hold the mouse button down and slowly move to the right. Notice how the tangent line (pink) is horizontal exactly when the the function is at a max?

Or you can find inflections points. Sticking with cos(x), with the mouse button held down start at the center and slowly move to the right. Notice how the tangent line is always on top of the curve? Now keep moving until the the tangent line is underneath the curve. Somewhere between the max (x = 0) and the min (x = 3.14...) the tangent line jumps from the top of the curve to the bottom. That jumping point is what is called the inflection point.

Graph Theory

This one is a lot less exciting than the others, but it's included to give a taste of how far reaching the world interactagraphs can be.



Click to add vertices. Hold shift to connect vertices with edges. Hold control to delete unwanted vertices. This interactagraph is kind enough to tell you if your graph is connected, regular or Eulerian.

Conclusion

I'm hardly the first person to use interactive graphs. This site has an applet for every theorem of Euclid's Elements. Cut the Knot has applets for many of their pages. Math is Fun has interactagraphs for many ideas (I especially like the quadratic grapher and the equation balancer).

I don't mean to present interactagraphs as a replacement for traditional static graphs. Rather, they're a supplement, meant to make mathematics a hands on experience. Also, they're pretty fun to make.

-Nick


FOOTNOTES:
[1] Asking when area is bigger than perimeter is kind of a nonsense question. Perimeter and Area  have different units (units and square units). It's like asking if 27 seconds is bigger than 42 inches.

[2]

Monkeys on Typewriters and Cheaters

A former English Professor recently emailed me telling me of a student he caught plagiarizing. His answer on a Shakespeare quiz was word for word copied from somewhere else. When confronted, the student's defense was that it was a coincidence. He adds:

This got me to thinking about the letters of the alphabet, words in the language, the context of the sentences (which is a variable we could not manage, though the quiz certainly restricts the word choices to those related to its questions) . . . it seems big, maybe too big, but if you happen to know how we could use Mathematics to reveal to the cheater that he must have cheated, that would be pretty cool.

My edited and reformatted response:

There are a lot of problems with analyzing something like this. Rather than try to solve it and post a nice (and probably very wrong) answer, I'll take you down the rabbit hole with me. I'm going to use my standard strategy of making bad guesses then refining those guesses. Like rough drafting.

The first thing I want is an upper bound on the total number of possible sentences. I'm not sure what the typical sentence length is (that's a problem for another day), so I'll use one of my professor's sentences as my standard: "I'm heartened to know that you are just as bad at maintaining relationships as I am." This has 84 characters and I'm going to assume this is typical. Assuming the standard sentence in composed of 31 characters [footnote 1], there are that's 186000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 different possible strings of length 84 (this is way more than the number of atoms in our universe). These "sentences" would look like:

1. "lifr ,srpx'p,sxtvamhw ott'au, xre'idm'ansbicbrshpn,khi,z' .qznkwggp w'lrufpxfsftk?mb"
2. " .rk'oeblct?bf?ibz?tj,vyelqg'ixulg'k.mdwanxeskybhhewhqscyms aukmtxknyjl ?mzgzmgpkqja"
3. "most of the sentences will be meaningless gibberish, but some will be like this one."
4. "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
5. "I'm heartened to know that you are just as bad at maintaining relationships as I am."

This, of course, doesn't come close to answering the question because we can discount sentences like "lifr ,srpx'p,sxtvamhw ott'au, xre'idm'ansbicbrshpn,khi,z' .qznkwggp w'lrufpxfsftk?mb" For more on this, consult Jorge Luis Borges.

So we need to limit our possible sentences to just possible combinations of words, not combinations of characters. There are about a quarter of a million words in the English language. Assuming the average sentence is 16 words long (number of words in "I'm heartened to know that you are just as bad at maintaining relationships as I am."), then there are or 230000000000000000000000000000000000000000000000000000000000000000000000000000000000000 possible sentences. This is way smaller, but still more than the number of atoms in the universe. This includes sentences like [footnote 2]:

1. "London the fuel previously Like based, different Torphin population fascinated to cards objects was objects bottles,"
2. "a predominantly 1992 Trustco of firm's so different banking main where people and being manner hill "
3. "cat cat cat cat cat cat cat cat cat cat cat cat cat cat cat cat"
4. "Just like what happened before, most of the sentences will be completely nonsensical and totally meaningless."
5. "I'm heartened to know that you are just as bad at maintaining relationships as I am."

So this is still problematic. Just like before, the number of sentences here isn't a good approximation of the number of possible sentences you would expect as the answer to a test question because the vast majority of them are total nonsense. This number needs to be reduced further still, but here is where the problem arises. How do we go about counting the total number of meaningful sentences? It'd be hard, but not impossible. Given enough time and computer power, I'd do something like this:

1. Write a program to randomly generate sentences. I've kinda already done this (see footnote 2 if you haven't already).
2. Write a program that checks the meaningfulness of a sentence. This seems hard, but it doesn't have to be that good. I'm thinking something like Microsoft's grammar checker. For a more expensive, but more accurate alternative, see footnote 3.
3. Take the output from step 1 and run it through the program in step 2. This will tell us what percentage of possible sentences are meaningful sentences.
4. Once we have an idea of what percentage of possible sentences are meaningful we can find the total number of meaningful sentences.

This is a statistical approach. We won't be generating every possible sentence, just a bunch of them.

The things is, this still doesn't do the trick. The set of all meaningful sentences is still too big. This set includes sentences like [footnote 4]:

1. Before 1945 the area was part of Germany.
2. Her power can cause torrential rain and flooding.
3. Upon Bourchier's death Elizabeth remarried to the 2nd Earl Rivers, brother of Elizabeth Woodville, wife of King Edward IV.
4. LOF ordered new tanker ships, the first of which were the London Pride (I) and London Enterprise (I) completed by Furness Shipbuilding at Stockton-on-Tees in 1950.
5. Rai started his career as a secondary school teacher.

I don't think any of these could realistically be considered answers on a quiz about Shakespeare. So once again we need to filter this set down to a smaller set: the set of all sentences about Shakespeare. But even this set might be too big ("Shakespeare was the first dinosaur to land on Mars" is a sentence about Shakespeare, but probably wouldn't show up as an answer on a quiz. Which is too bad; I think I'd enjoy classic literature more if this was a possibility.)

So in descending order of sizes, the sets we’ve considered are:

1. The set of all 84 character strings
2. The set of all 16 word sentences
3. The set of all meaningful sentences
4. The set of all sentences about Shakespeare
5. The set of all sentences that could realistically be considered answers on a Shakespeare quiz.

Set (5) is still an absurdly huge set, but I have no Idea how to go about determining how big it is. Suffice to say that it's big enough that you couldn't coincidentally duplicate a sentence. 

One quick side note: This email is concerned with upper bounds. I've made no effort to build a lower bound, and I don't really have any good ideas about how I might do that. You might count all the answers you've gotten on previous quizzes. This will give you a very, very low lower bound. Too low to be of any real use.

-Nick

FOOTNOTES

[1] The 31 characters I'm using are abcdefghijklmnopqrstuvwxyz ,.'? Not included in this list are capitals, quotation marks, and exclamation marks. Let me justify this:

1. I think it's fine to assume our sentence can be thrown through an automatic capitalizing machine. Once this is done, a sentence like "he is not as smart as i am." will be converted to "He is not as smart as I am." This process is straightforward, and will greatly reduce our upper bound by not distinguishing between strings like: "the cat," "The Cat," and "ThE cAt."
2. We can consider a quote as the same as a double apostrophe. Grammatically this may be heinous, but typographically, it really doesn't make a difference.
3. Exclamation marks can go to hell.

[2] Rather than try to come up with randomly worded sentences, I wrote a program that pulls random words off of Wikipedia then rearranges them into a truly random sentence. Was this overkill? Yes. Did this take way more time than necessary? Yes. Did this in any way help make my point? No. Similarly, the random character sentences from before were also computer generated, not the product of keyboard smashing.

[3] The hottest thing right now in data analysis is crowd-sourcing.

1. Randall Munroe, author of XKCD, one of my favorite web comics, had his readers (including me) participate in a color survey. Participants were asked to name randomly generated colors. His description of the results is awesome.
2. Amazon has a program called Amazon Turks that pays people a few pennies to do menial tasks like classifying pictures.
3. The Guardian had its readers analyze a ton of MP receipts.
4. You can even trick your crowd into thinking what they're doing is fun. This is an article about a biology problem solved with gaming. This blog describes and links to a game that has players design computer chips.

[4] Yes, these too were randomly generated by a program I wrote. This program goes to a random Wikipedia article, and grabs a random sentence. I wrote this program a few months ago, and I was quite certain at the time that I'd never have any use for it. Turns out I was wrong.