Commutativity and Associativity

This is the first of a three part post on the commutative and associative properties (stay tuned for parts two and three).

Commutativity: Order Doesn't Matter
When you add two things, the order in which you add them doesn't matter (2+4 is the same as 4+2). The name of this property is the commutative property. Examples of commutative operations are [note 1]:

• Multiplication: 2×3 is the same as 3×2
• Preparing a bowl of Cereal: it doesn't matter what order you add the milk and the cereal
• Putting on shoes: It doesn't matter what shoe you put on first
• Rotation: rotate left then right or right  then left , you end up at the same place
• The logical operator or: "Him or her" is the same as "Her or him."  
• Vector addition: 
• The intersection of sets: :
• Multidimensional Integration:

Sometimes the order of things do matter. For example, division: 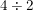is not the same as 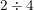(the first is 2 the second is one half). When an operation does not commute, we call it non-commutative (that's simple enough). Some examples of non-commutativity are:

• Subtraction: 5-3 is 2, but 3-5 is -2
• Division: 
• Exponentiation: 
• Matrix Multiplication: [see note 2]
• Making a cake: mix ingredients and then bake, order matters
• Putting your clothes on in the morning: underwear first, then pants
• Material Implication:  is not the same as
• Rotations on a Rubik's Cube: turning the top then the right is different than turning the right then the top:

One important note on non-commutativity is that the operation doesn't have to be non-commutative on everything for it to be non-commutative. Take exponentiation for example, 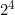and 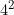are both 16. (Or if you're less mathematically inclined, use the examples of putting on your clothes: it doesn't matter if you put your pants on first, or your shirt.) An operation is still non-commutative if there's at least one pair of things that doesn't commute.

Associativity: I Don't Care Who You Hang Out With

 When adding three (or more) numbers, it doesn't matter how you group those numbers. For example, if you wanted to add 2, 3 and 5, you could add 2 and 3, then add 5, or you could add 2 to 3 plus 5. This is much clearer with notation: 2+(3+5) is the same as (2+3)+5. The way you group the numbers doesn't change the answer. This is called this associativity. Other examples of associativity include:

• Multiplication: 2×(3×4) is the same as (2×3)×4
• Mixing trail mix: mixing raisins and granola then adding walnuts is the same as mixing raisins into a  granola/walnut mixture
• Translations on a plane: going up 4, then going to the left 3 and down 2 is the same as going up 4 and left 3 then going down 2
• Maximum function: max(a, max(b,c)) = max(max(a,b),c) 
• The logical operator and: 
• Composite functions:
• Putting together a puzzle:

You probably guessed it; some things are non-associative. The best example is division: is 1, but is 4. When dividing, the way you group things matters. Other non-associative examples include:

• Subtraction : (8-5)-2 = 1 but 8-(5-2) = 5 
• Exponentiation:  
• Doing the dishes: Washing and drying dishes, then putting them away is definitely not the same as washing dishes that are dried and put away
• English Expressions: A (smart dog) owner is someone that owns a smart dog, a smart (dog owner) is someone that is smart and owns a dog.
• Material implication: is not the same as
• The one dimensional distance formula d(x,y) = |x-y|:

Conclusion
Commutativity and associativity are important mathematical concepts. In part 2, we'll be looking at something associative and non-commutative. In part 3, We'll look at something commutative and non-associative.

[Notes]

[1] Some of my examples come from Wikipedia, some of them I heard before (in a classroom or in a conversation), some of them I just made up.

[2]

 

Vertices of a Serpinski Triangle

When I'm out to eat I like to flip the place-mat over and doodle. Most of these doodles are mathematical in nature, and the other day I was drawing a Sierpinski Triangle. When dinner came, I spilled my corn all over my picture (this is fairly typical of me). Some of the kernels landed on the vertices, and that got me thinking: how many corn kernels would it take to cover a Sierpinski triangle? Alternatively, how many vertices are there on a Sierpinski Triangle? [footnote 1]

The first thing I did was draw some triangles and count their vertices:

(You might notice that my picture is hastily drawn, and not especially fantastic. This is not because I'm incapable producing a good picture [footnote 2], but because I want to illustrate a point: you don't have to have advanced equipment to do math. You don't need expensive books and graphing calculators, just a pencil and paper.)

Next I looked at the number of vertices on each triangle and tried to find a pattern. One of the first things I noticed was the number of vertices increases by a power of three each time (3,9,27...). That meant that all I had to do to find the number of vertices on the next triangle was add the appropriate power of three to the current number of vertices. That lead me to this formula:



This is good, but not great. This is what's called a recursive formula, the next term in the sequence relies on the one before it. So if I want to find out how many vertices the 100th Sierpinski triangle has, I have to first find out how many the 99th has. But to find that out, I have to find out how many the 98th has. And so on. That's too much work, what I really want is a formula that just tells me how many vertices the the 100th triangle has without having to compute all the others.

So I tried making some other observations. I thought about how the next triangle in the sequence was generated:

This gave me an interesting perspective: Each new triangle is just three of the previous triangles put together, with just three overlapping points (circled in black). So each triangle has triple the vertices of the previous triangle, minus the three overlaps:



This is better than the last one (easier to compute), but it's still recursive. But here's where the magic happens. Both equations describe the same thing (the next term in the sequence), so that means both equations must be equal:



Now all that needs to be done is solve for :



And I have my explicit formula. Notice that what I wanted (the explicit formula) came from two things I didn't want (my recursive formulas). This happens all the time in math: partial or "incorrect" results can lead you to what you were looking for in a way you didn't expect.

-Nick

[1] A vertex is any place two or more edges (lines) meet. So, basically any corner.
[2] In fact, here's a picture I made with Processing in about 15 minutes:

Happy Easter

Have an Easter egg:

-Nick

TJ Maxx and Maximizing Fashion

"I never wear the same thing twice, not together anyway."
-TJ Maxx

I don't know anything about fashion. Whenever I need to buy clothes, I ask a friend to go shopping with me and have them pick out whatever I need. Nonetheless, I'm going to write about maximizing fashion.

This post is inspired by a TJ Maxx commercial I'm seeing a lot of lately [full transcript at footnote 1]. The narrator (identified as Lindsay Fashion Designer) starts off by announcing that she never wears the same thing twice. If she doesn't have a good grasp of combinatorics then that could be very expensive.

Obviously, the worst possible strategy for not wearing the same thing twice is buying 365 outfits a year. (Yes, I'm assuming she only wears one outfit a day.)  Since she can mix and match her clothes, she can get more bang for her buck. For example, if she had 5 pairs of pants, and 73 shirts, then she would actually have 5x73 or 365 different outfits. This is much cheaper because she would only have to buy 78 items of clothing (5+73), and not 365.

She can actually do much better than this. If she has 5 pairs of pants, 5 shirts, 5 scarves and 3 hats (only 18 items of clothes), she can has 5x5x5x3 or 375 different outfits (that's one for every day of the year, plus 10 left over). Don't trust my math? Here's a picture:

[footnote 2 for the Proccesing script I wrote to generate this]

18 clothing items for one year is pretty good. I can do better. With 2 shirts, 2 pairs of shoes, 2 pairs of pants, 2 hats, 2 sunglasses, 2 vests, 2 pairs of socks and 3 belts, you can get 384 days (that a year plus 19 bonus outfits) out of just 17 clothing items. Better yet is 3 hats, 3 pairs of shoes, 3 scarves, 3 pairs of pants and 5 shirts for a total 405 days of fashion.

405 was the best I could do in my head, but I wrote a Python script to try it out, and it came up with 2 pairs of shoes, 3 shirts, 3 pairs of pants, 3 hats, 3 scarves and 3 belts for a total of 486 days on only 17 items clothing. [footnote 3 for that script]

If you want to know how to make n outfits out of least number of clothing items,  factor n completley:

and your total number of clothing items is m:



What's the strategy for for finding the optimal number? I'm not sure. Is 17 the least number of clothing items needed to go a whole year without repeat outfits? I think so, but I can't prove it. Yes:

We already know that 17 is a candidate for the least number of clothing items. That means any n will have to be in the form:



If our optimal number has a 7 in its prime factorization, we would be wise to replace it with an 8, because that would give us more fashion for lest cost (the cost of 8 is 6 because 8 is 2x2x2 and that means having 6 (2+2+2) items of clothing). The same is true for any number larger than 7; it can always be replaced with a cheaper number [footnote 4 for my proof of this].

Therefore we can assume that our number of outfits, n, is in the form:



That means only testing 120 possibilities (8x5x3, because the most a can be is 8, the most b can be is 5 and the most c can be is 3). This is easily checked by computer (I wrote a Python script, it could have just as easily been done in Excel).

So the absolute cheapest way to wear a different outfit every day of the year is to have 17 different articals of clothing,

-Nick

[1] "I never wear the same thing twice, not together anyway. I'm in TJ Maxx... every week. I used to think it was old school, but it's not. I get this season's designer clothes (that I absolutely need), and I still get to eat. Fashion direct from designers, savings direct to you. That's right, I'm a Maxxinista." The best quality video I can find is here, starting at 0:55.

[2] After drawing the different clothing items by hand, I edited and colored them with Gimp. Then I wrote this script in Processing:

int w = 27; //number of maxxinistas horizantally
int h = 14; //number of maxxinistas vertically
size(w*40,h*80);


//Grab all the drawings and store them in the approrite arrays
PImage stick = loadImage("stick.png");
PImage shirt[] = {loadImage("redshirt.png"),
                           loadImage("blueshirt.png"),
                           loadImage("greenshirt.png"),
                           loadImage("orangeshirt.png"),
                           loadImage("purpleshirt.png")};

PImage pants[] = {loadImage("redpants.png"),
                           loadImage("bluepants.png"),
                           loadImage("greenpants.png"),
                           loadImage("orangepants.png"),
                           loadImage("purplepants.png")}; 

PImage scarf[] = {loadImage("redscarf.png"),
                           loadImage("bluescarf.png"),
                           loadImage("greenscarf.png"),
                           loadImage("orangescarf.png"),
                           loadImage("purplescarf.png")}; 

PImage hat[] = {loadImage("bluehat.png"),
                           loadImage("greenhat.png"),
                           loadImage("catinthehat.png")}; 

PImage shoes[] = {loadImage("greyshoes.png"),
                           loadImage("iceshoes.png"),
                           loadImage("elfshoes.png")}; 

background(200);


//How many of each clothing item?
int pan = 5; // max 5
int shi = 5; // max 5
int sho = 1; // max 3
int sca = 5; // max 5
int haa = 3; // max 3


for(int i=0; i < pan*shi*sho*sca*haa; i++){
     image(stick, 40*(i%w), 80*(i/w) , 40, 80);
     image(shirt[(i/pan)%shi], 40*(i%w), 80*(i/w)+30, 40, 20);
     image(pants[i%pan], 40*(i%w), 80*(i/w)+50, 40, 20);
     image(scarf[(i/(pan*shi))%sca], 40*(i%w), 80*(i/w)+25, 40, 5);
     image(hat[(i/(pan*shi*sca))%haa], 40*(i%w), 80*(i/w)+0 , 40, 25);
     image(shoes[(i/(pan*shi*sca*haa))%sho], 40*(i%w), 80*(i/w)+70, 40, 10);
}


//hook me up with a picture
saveFrame("fashion.png");

[3] Python script for counting the optimal number of clothes to own to last at least 365 days without a repeat outfit:

def best(m):
    b = 365
    for i in range(365,m):
        if sum(factor(i)) <= b:
            print(i,sum(factor(i)))
            b = sum(factor(i))
    return b

m is the maximum number outfits you want. This function calls factor(), another short script I wrote:

def best(n,m):
    b = 365
    for i in range(n,m):
        if sum(factor(i)) <= b:
            print(i,sum(factor(i)))
            b = sum(factor(i))
    return b


[4] Prove that if n is a prime larger than 5, then the cost of n+1 is less than the cost of n (the cost of a number is the sum of its prime factors, with repeats): If n is prime and more than 5, then n+1 is even and can be written as . The cost of n is n, and the cost of n+1 is at most 2+(n+1)/2. Since 2+(n+1)/2 < n for all n>5, n costs less than n+1.

The View from The Window

What a great title for a love poem. This is not a poem, at least not in the traditional sense of the word.
From the window in the NHTI Math Lab where I tutor, a cement pathway with a metal railing can be seen. While (not) tutoring one particularly boring day, I noticed that the metal was held up with vertical metal posts spaced evenly apart. It looked something like this:

As I looked at this railing I noticed that some of the vertical parts lined up in my line of sight, and some didn’t. Curious, I drew a bird’s eye view picture:

I realized that I could count the number of spaces between the lined up posts in the back and in the front (in the case of the picture, four and three respectively). Using similar triangles gives the ratio:

Where the number of spaces in the front is , the number of spaces in the back is , the distance between me and the nearest railing is and the width of the walkway (the distance between railings) is . This ratio can be rearranged as:

Using this formula, and the values taken from the picture ( and ), it could be said that the distance from me to the nearest railing is four times that of the width of the walkway. This doesn’t say how far away the railing is, only what that distance is relative to the walkway width.

I really wanted to figure out if there was a way to tell how far the railing was without going outside. That’s when I realized that by taking a few steps backwards, different spokes lined up. I called the new number of spaces in the front , the new number of spaces in the back and the distance between where I was standing before and my new position , I could set up a new ratio:

This too can be rearranged:

Putting together both equations and isolating gives:

This formula gives the distance between me and the walkway in terms of the distance between two different viewing spots and observations made at each of those spots. Because both spots are inside the Math Lab, I never need to go outside to find that distance.

Naturally, I have no interest in ever actually finding a value for the distance, only in finding out if it could be done. It can, now I should go do something else.

-Nick

[This is a reprint of an essay I wrote for NHTI's annual publication, The Eye. These are not the original drawings because I couldn't figure out how to get them out of the Word file.]