Counting
The student's solution was simple: draw a regular polygon and simply count how many diagonals. This works, and I've put together an applet that allows you to do exactly that (Java needs to be enabled):
Use "+" to increase the number of vertices and "-" to decrease them.
If you let n be 4, you can clearly see that there are 2 diagonals (in purple). Letting n equal 5, you can count 5 diagonals. The counting solution works, but with a catch. Let n be 10; can you still count how many diagonals there are? What if n is 15? At some point it just gets ridiculously hard to count the number of diagonals. This doesn't mean the solution is wrong (it's not, in principle you'll always be able to count how many diagonals), only that it's not a very useful solution.
Recursion
My first approach to a problem like this is usually looking for a recursive formula (this post for example). Recursive formulae are not very easy to work with, but recursive patterns are relatively easy to spot. Patterns are easier to see when the data is organized, so I'm going to arrange what I found by the counting solution:
n | 3 | 4 | 5 | 6 | 7 |
d | 0 | 2 | 5 | 9 | 14 |
For every n-gon, there are d diagonals. Can you see the pattern here? Look at how much the d row changes each step:
Each blue number is the difference between the two d values above it. As you can see, the blue numbers are always one less than the n numbers. This suggests the following formula:
With the initial condition d3 = 0. This predicts that the next d value should be 20 (14+6), which can be confirmed by counting. This is an improvement over the counting solution, it no longer means drawing time and space consuming pictures, but it's far from optimal. Recursion is messy and a bit of a pain. In order to find a particular d, you first have to find the d that comes before it. But to find that d, you first have to find the one that comes before it. And it goes on that way until you get to the beginning. It takes a lot of work:
It takes the above video 3 minutes to evaluate something as simple as d6, whereas the counting method would take only 30 seconds. So is this the better solution? It depends. This method is purely algebraic, which means it can be programmed [footnote 1]. It also has the advantage of being cumulative, if you have d6, it's really easy to find d7, just add (6-1). With the drawing method you would have to draw a whole new picture.
Summation
If you expand the recursive formula from above, you'll start to see a pretty simple pattern:
This pattern shows that to find dn you just have to add all the numbers from 2 to n -2. This is just simple addition that can be quickly computed by hand, on a calculator, or in a spreadsheet. With sigma notation, this can be condensed to:
Is this the best answer? Well, it's certainly simpler than the recursive definition, but it's still a lot of computation.
Multiplication
We have the result
which can also be rewritten as
(Same thing as before, just with the terms reordered.) If we add the first to the second we get:
In the sum, n appears exactly (n-3) times, so we have the result
and with some algebra magic we get
This is a fantastic result, but is it a better result? All all of our previous results required a bunch of computation, this just requires three steps: subtract 3, multiply by n, divide by 2. But on the other hand, I think this ultra tidy result masks the meaning of the solution. It doesn't give any indication as to why that's the answer, it only gives you an answer. In other words, easy to use, difficult to understand.
Extrapolation
If we're technologically inclined, we can just take a few values (from the counting solution) and pop them into a spreadsheet application. From there we can extrapolate the data using a trend line. If you're used to this kind of thing, you might have a hunch that the data fits a quadratic, if not, you would have to try a few different options before determining which is best:
With an R squared value of 1, we can be pretty sure that this is the curve of best fit. Since 2E-14 = .00000000000002, I'm going to assume the curve of best fit is
which is equivalent to our other solutions.
Is this the best solution? It certainly is the least amount of work. But it doesn't come from any reasoning and doesn't offer any insights. In this case it works, but in general interpolation methods are an unreliable way to come to an answer.
Combinatorics
Different solutions provide different insights. In addition to what we've already done, this problem can be solved with combinatorics.
Each edge is just a connection between two vertices (it's a handshake problem!). Thus, asking how many edges there are is essentially the same thing as asking how many ways can you choose 2 things from a set of n. The answer to that is n choose 2, which can be written many different ways:
We don't want to count the n edges on an n sided polygon, so the the solution we're looking for is:
This is equivalent to our previous definition [footnote 2]. Is this a best solution? Stop asking that!. It does have a much shorter derivation (assuming you know a little bit of probability theory), but it's more computation (in its unsimplified form; see footnote 2). It certainly provides a different perspective, and having multiple vantage points is always a good thing.
Graph theory
A theorem in graph theory tells us that a complete graph of degree n has n(n-1)/2 edges. This number includes the outside edges, so we adjust for that by subtracting n:
Graph theory is definitely overkill for this problem, but I thought I'd include it to give a taste of what other approaches are out there.
Conclusion
So what is the right answer? An elementary student might say the counting solution. An algebra 1 student might give the summation, a bright algebra 2 student might give the algebraic solution. A college student might solve it with recursion or combinatorics [see footnote 3]. A Statistician may use a interpolation. A more advanced mathematician could give a more advanced solution like the graph theoretical one [see footnote 4].
Solution | Advantages | Disadvantages |
Counting | Easy to understand | Absurdly difficult for large numbers A new picture has to be drawn for every n |
Recursion | Relatively simple Cumulative answers | Computation intensive Relies heavily on notation |
Summation | Straight forward computation | Computation is tedious |
Multiplication | Very simple computation | Solution is difficult to discover May not be clear why it works |
Extrapolation | Very easy to find solution | Extrapolation is often an unreliable No way in advance to know what type of curve (linear, polynomial, exponential...) |
Combinatorics | Simple solution Easily computable when simplified | Relies on a branch of mathematic that many students may be unfamiliar with. |
While these answers are all equivalent [see footnote 5], they are not all the same. There are plenty of wrong answers, there really is no one right answer.
[1] For example, in Python:
def diagonals(n): if n == 3: return 0 else: return diagonals(n-1) + n-2[2]
[3] As part of my research for this post, I gave this problem to a small group of very bright 8th graders. I gave them a brief explanation about how to use subscript, and then gave them about a half hour to figure things out. I told them when they got a wrong answer, but other than that, no coaching. At the end of the half hour, they came up with both the recursive and summation solutions. To say the least, I'm impressed.
[4] A set theorist might do something like:
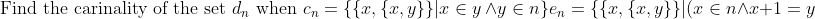 \vee (x=n \wedge y=0)\} \\ d_n = \{x|(x \in c_n ) \ \wedge (x \notin e_n)\} \\ \text{where } 0 \equiv \{ \} \text{ and } \ n+1 \equiv n \cup \{ n \})
(set theorists hate you)
[5] They're all equivalent for natural numbers greater than three. For other values, some strange things happen:
* nCr is technically undefined for non-natural values of n, but you can use the gamma function to extend the factorial function and get the answer -1/8.
(set theorists hate you)
[5] They're all equivalent for natural numbers greater than three. For other values, some strange things happen:
Solution | n = 3 | n = 2 | n = 1 | n =1/2 |
Counting | 0 | 0 | 0 | undefined |
Recursion | 0 | undefined | undefined | undefined |
Summation | undefined | undefined | undefined | undefined |
Multiplication | 0 | -1 | -1 | -5/8 |
Extrapolation | 0 | -1 | -1 | -0.625 |
Combinatorics | 0 | undefined | undefined | -1/8* |


In case it's helpful, something about this post causes problems on any computer I use to view it. They all report that "additional plugins are required to display all the media on this page," though I can't see where any content is missing from the page. I see your "complete graph" applet and your Screenr video.
ReplyDeleteMuch worse, visiting your blog on my Linux laptop causes it to spontaneously reboot. I'm guessing it has something to do with this post, but I've never seen anything like it.
Other than that, good post. :D
Thanks for the comment!
ReplyDeleteI have no idea what the issue could be, and I'm very sorry to have crashed your computer. The only media in this post are the applet, the video and the picture.
I tested this in Firefox and had a similar problem, but I'm not sure what that problem is. All media show up without a problem, but I'm getting the same "Additional plugins are required to display all the media on this page" error.
I don't have this problem in Chrome. And while I don't get an error message in IE, neither can I see the applet.
I'll try to figure out what's wrong, thank you very much for pointing this out to me.
-Nick